Chapter 6 Factorial experiments
In this section, we consider experiments where the treatment structure involves multiple experimental factors.
6.1 Combining factors: Crossed vs. nested designs
There are two distinct ways in which experimental factors can be combined. The distinction is illustrated by the following two experiments
Experiment 1. (A hypothetical experiment based on example 15.8 in Ott & Longnecker):
A citrus orchard contains 3 different varieties of citrus trees. Eight trees of each variety are randomly selected from the orchard. Four different pesticides are randomly assigned to two trees of each variety and applied according to recommended levels. The same four pesticides are used for each variety. Yields of fruit (in bushels per tree) are recorded at the end of the growing season.
Experiment 2. A study is conducted to investigate the effect of pest management practices on cotton in the central valley of California. 14 ranches are available for study. Each of the 14 ranches is managed by one consultant.
In both experiments, there are two experimental factors—variety and pesticide in experiment 1, and consultant and ranch in experiment 2. Each unique combination of factors forms a separate treatment combination. In experiment 1, the treatment combinations are formed by crossing the two experimental factors. That is to say, every level of the first factor (variety) is combined with every level of the second factor (pesticide). This is an example of a factorial or crossed design. In experiment 2, each level of one factor (ranch) is only combined with one single level of the other factor (consultant). This is an example of a hierarchical design, and we would say that ranch is nested within the consultant.
Experiments with more than two factors can give rise to designs that involve aspects of both crossed and nested designs. For example, if we three factors—call them factors “A”, “B”, and “C”—we might cross factors A and B and then nest factor C within the A*B cross.
The remainder of this chapter concerns factorial designs. We will begin by studying a two-factor cross. Most of the ideas involved in analyzing factorial designs can be mastered by studying a two-factor cross. We will conclude this chapter with a three-factor design to see how ideas from two-factor designs extend to experiments with more than two factors.
The analysis of factorial designs makes heavy use of the idea of contrasts, so make sure you understand that material well.
6.2 2 \(\times\) 2 factorial design
We will first study the simplest of all factorial designs, a 2-by-2 cross. We will then progress to two-factor crosses in which each factor may have an arbitrary number of levels.
In a two-factor design, the two factors can be generically labeled as factors “A” and “B”. The scientific questions of most interest in a two-factor design are:
Does the average response differ among the levels of factor A, and if so, how?
Does the average response differ among the levels of factor B, and if so, how?
Do the differences among the levels of factor A depend on the level of factor B, and vice versa? If so, how? That is to say, is there evidence of an interaction between the two factors?
6.2.1 Example: Weight gain in rats
Consider the following example taken from Sokal and Rohlf (1995). This experiment was designed to examine differences in food consumption among rats. 6 male rats and 6 female rats were used in the experiment. Half the rats were fed fresh lard (fat), and half the rats were fed rancid fat. The response is total food consumption (in grams) over 73 days. This is a 2 \(\times\) 2 factorial design with a CRD. The experiment is balanced.
Here is some notation that we will use for two-factor experiments:
\(a\): number of levels of factor “A” (here, we’ll set ‘sex’ as this factor, so \(a = 2\).)
\(b\): number of levels of factor “B” (here, we’ll set ‘fat’ as this factor, so \(b = 2\).)
\(i = 1, 2, \ldots, a\): an index to distinguish the different levels of factor A (\(i = 1\) for males, \(i = 2\) for females)
\(j = 1, 2, \ldots, b\): an index to distinguish the different levels of factor B (\(j = 1\) for fresh fat, \(j = 2\) for rancid fat)
\(n_{ij}\): sample size for the combination of level \(i\) of factor A and level \(j\) of factor B (in a balanced design, sometimes this gets replaced by \(n\)).
\(k = 1, 2, \ldots, n_{ij}\): an index to distinguish the different observations within each treatment combination
\(y_{ijk}\): \(k\)th observation from the combination of level \(i\) of factor A and level \(j\) of factor B.
\(n_T =\sum _{i=1}^{a}\sum _{j=1}^{b}n_{ij}\) : total sample size
\(\bar{y}_{ij+} =\dfrac{\sum _{k=1}^{n_{ij}} y_{ijk}}{n_{ij}}\): sample mean for the combination of level \(i\) of factor A and level \(j\) of factor B
\(\mu_{ij}\) : unknown population mean for the combination of level \(i\) of factor A and level \(j\) of factor B
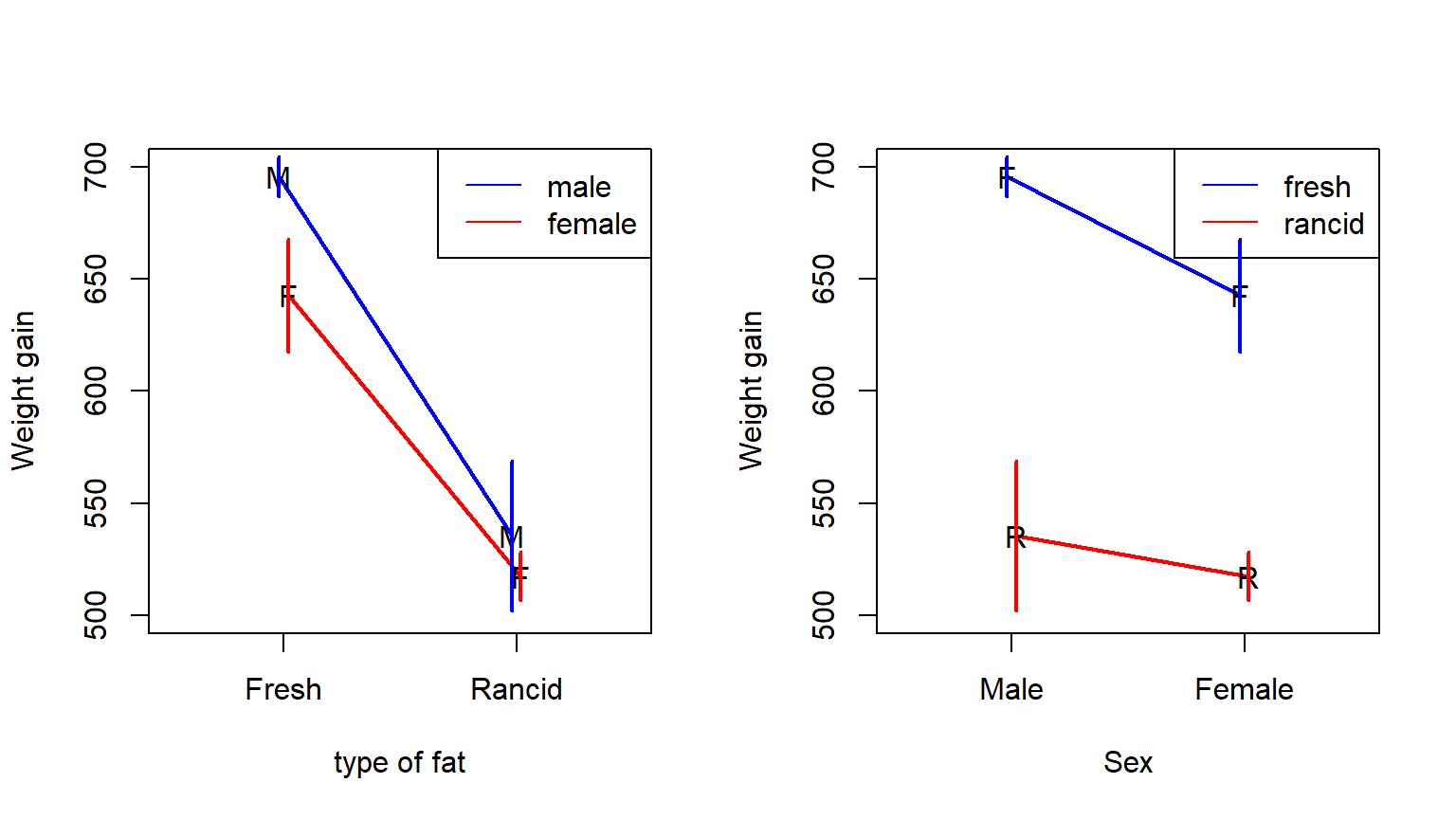
Figure 6.1: Interaction plots of the rat weight-gain data
Notice how the two versions of the plot show the same information but emphasize different comparisons. Which version you prefer is a matter of taste.
6.2.2 Two-factor ANOVA hypothesis tests
The traditional approach to analyzing a two-factor design is through a two-factor ANOVA. A two-factor ANOVA uses the variation among the group means to test for differences in the mean response across the levels of each factor and for an interaction between the factors.
To understand these comparisons, it is useful to have some additional terminology. We define the average responses associated with each treatment combination (what we have written above a \(\mu_{ij}\)) as cell means. (The name “cell mean” arises from the fact that we often think of each treatment combination as corresponding to a “cell” in a table in which each factor corresponds to one of the table’s dimensions.) A marginal mean is the average of all the cell means associated with one level of one factor, averaged over all the levels of the other factor(s). For example, in the rat weight-gain data, the marginal mean associated with the male rats is \[ \bar{\mu}_{1+} = \dfrac{\mu_{11} + \mu_{12}}{2}. \] Here, we’ve used the notational convention of using a plus (+) subscript to indicate that we are summing over the levels of an index. Similarly, the marginal mean associated with rats fed fresh fat is \[ \bar{\mu}_{+1} = \dfrac{\mu_{11} + \mu_{21}}{2}. \]
6.2.2.1 Comparisons of marginal means
The two-factor ANOVA provides \(F\)-tests to test for differences among the marginal means of each factor. In the rat example, one \(F\)-test tests the null hypothesis that there is no difference between the marginal means for male and female rats: \[ H_0: \bar{\mu}_{1+} =\bar{\mu}_{2+} \] and another \(F\)-test tests the null hypothesis that there is no difference between the marginal means for the two tupes of fat: \[ H_0: \bar{\mu}_{+1} =\bar{\mu}_{+2}. \] When there are more than two levels of one or both of the factors, these \(F\)-tests correspond to tests of equality of all the marginal means. For example, when there are more than two levels of factor “A”, the ANOVA \(F\)-test of this factor corresponds to the null hypothesis \[ H_0: \bar{\mu}_{1+} =\bar{\mu}_{2+} = \ldots = \bar{\mu}_{a+}. \]
Notice that each of these null hypotheses corresponds to a contrast of the cell means. It may take a little work to see this, but we can do it. For example, our test for a difference between the marginal means of the two types of fat can be re-expressed as the contrast \[ \begin{align} \theta & = \bar{\mu}_{+1} -\bar{\mu}_{+2} \\ & = \dfrac{1}{2}\mu_{11} + \dfrac{1}{2}\mu_{21} - \dfrac{1}{2}\mu_{12} - \dfrac{1}{2}\mu_{22}. \end{align} \]
Because there are only two types of fat, the comparison between the two marginal means is a simple contrast. More generally, the test for the equality of \(a\) marginal means is a complex contrast that involves \(a-1\) linearly independent (or non-redundant) simple contrasts.
We will sometimes refer to comparisons of marginal means as the main-effects comparisons associated with a particular factor.
6.2.2.2 Interaction
To think through the interaction, it is helpful to have a bit more terminology at our disposal. We define the simple effect of a factor as the comparisons among the levels of one factor within the level(s) of the other factor(s). For example, in the rat experiment, the simple effect of type of fat for male rats is the comparison between male rats fed fresh fat vs. male rats fed rancid fat. In our notation, this corresponds to the difference \[ \theta_{\mbox{fat:male}} = \mu_{11} - \mu_{12}. \] Note that this simple-effect comparison is a simple contrast of the cell means. Similarly, we can define the simple effect of fat type for female rats as the comparison between female rats fed fresh fat vs. female rats fed rancid fat, or, in notation, \[ \theta_{\mbox{fat:female}} = \mu_{21} - \mu_{22}. \]
An interaction is a comparison of simple effects. In the rat data, the ANOVA \(F\)-test of the interaction corresponds to a test of \[ H_0: \theta_{\mbox{fat:male}} = \theta_{\mbox{fat:female}} \] or \[ H_0: \mu_{11} - \mu_{12} = \mu_{21} - \mu_{22}. \] Just as with regression, interactions go both ways: if the differences between the types of fat differs between male and female rats, then it also must be true that the differences between male and female rats depends on the type of fat. Notice also that, yet again, our test for an interaction can be expressed as a (in this case, simple) contrast of the cell means.
The interaction plots in Figure 6.1 are helpful for visualizing what is meant by an interaction. Consider the interaction plot on the left of Fig. 6.1 (with type of fat on the horizontal axis). The simple effect of type of fat for male rats corresponds to the left-vs-right comparison for the blue (male) line. The simple effect of type of fat for female rats corresponds to the same left-vs-right comparison for the red (female) line. The interaction asks if these two simple effects are the same or different for male vs. female rats.
Alternatively (and continuing to use the interaction plot on the left of Fig. 6.1), the simple effect of sex with fresh fat corresponds to the blue-vs-red comparison on the left of the plot. The simple effect of sex for rancid fat corresponds to the same blue-vs-red comparison on the right of the plot. The interaction asks if these two simple effects are the same or different for fresh vs. rancid fat.
6.2.2.3 Main-effects as averages of simple effects
Now that we are equipped with the idea of simple effects, notice that we can also define the main-effects comparisons as the averages of the simple effects. For example, the difference between the marginal mean for rats fed fresh fat vs. the marginal mean for rats fed rancid fat is just the average of the simple effects for type of fat in male and female rats. With this recognition comes a crucial point: If the interaction is significant, then we need to be careful about analyzing the main effects, because the main effects are averaging over simple effects that we know to differ. Thus, the conventional approach to analyzing two-way factorial classifications is to inspect the interaction first. If the interaction is not significant, proceed to analyze main effects of each factor. If the interaction is significant, then analyze simple effects, and interpret the main-effects comparison cautiously.
6.2.2.4 Sum-of-squares decompositions
To sum up so far: the two-factor ANOVA generates three \(F\)-tests: one to test for the equality of marginal means for the first factor, one to test for the equality of marginal means for the second factor, and one to test for the interaction between the two factors. Each of these tests are (possibly complex) contrasts. The tests of these contrasts proceed by computing the sum-of-squares for each contrasts and comparing this to the error sum-of-squares in the usual way. The number of “free differences” (or linearly independent contrasts) associated with each contrasts is| source | df |
|---|---|
| Factor A | \(a-1\) |
| Factor B | \(b-1\) |
| A*B interaction | \((a-1)(b-1)\) |
| Error | \(n_T-ab\) |
| Total | \(n_T-1\) |
Another way to think about this is that (for example) there are \(a\) marginal means for factor A, hence there are \(a-1\) differences among those means. For the interaction, there are \(b-1\) ways in which the \(a-1\) differences among the levels of factor A can differ among the levels of factor B; hence, the interaction entails \((a-1)(b-1)\) free differences (or linearly independent contrasts).
Just as with a one-factor ANOVA, the sums-of-squares in a balanced two-factor ANOVA can be computed using computing formulas that involve nothing more than addition, subtraction, multiplication, and division. These computing formulas were more important in the days before the advent of desktop computing. While there may be some small historical value to seeing how this worked, we won’t be computing these quantities by hand today. The formulas follow for completeness, but don’t feel compelled to study them.
The computing formulas begin with the usual one-factor SS decomposition: \[\begin{eqnarray*} \mbox{Total variation: } SS_{Total} & = & \sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{n_{ij} }\left(y_{ijk} -\bar{y}_{+++} \right)^2 \\ \mbox{Variation among groups: } SS_{Groups} & = & \sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{n_{ij} }\left(\bar{y}_{ij+} -\bar{y}_{+++} \right)^2 \\ \mbox{Variation within groups: } SS_{Error} & = & \sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{n_{ij} }\left(y_{ijk} -\bar{y}_{ij+} \right)^2 \end{eqnarray*}\]
Next, these formulas decompose the \(SS_{Groups}\) into three separate SS: one for each of the two main effects, and one for the interaction. Formulas for these sum-of-squares are: \[\begin{eqnarray*} SS[A] & = & \sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{n_{ij} }\left(\bar{y}_{i++} -\bar{y}_{+++} \right)^2 \\ SS[B] & = & \sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{n_{ij} }\left(\bar{y}_{+j+} -\bar{y}_{+++} \right)^2 \\ SS[AB] & = & \sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{n_{ij} }\left(\bar{y}_{ij+} -\bar{y}_{i++} -\bar{y}_{+j+} +\bar{y}_{+++} \right)^2 \end{eqnarray*}\] where SS[AB] denotes the sum-of-squares for the interaction. The formulas for SS[A] and SS[B] should make some sense: they consist of squared differences between the marginal means for one level of an experimental factor and the grand mean. The formula for SS[AB] is a bit more mysterious. Heuristically, the idea is this: with some algebra, the null hypothesis for no interaction \(H_0\): \(\mu_{ij} -\bar{\mu}_{++} =\bar{\mu}_{+i} -\bar{\mu}_{++} +\bar{\mu}_{+j} -\bar{\mu}_{++}\) can be re-written as \(H_0\): \(\mu_{ij} -\bar{\mu}_{+i} -\bar{\mu}_{+j} +\bar{\mu}_{++} =0\). Thus, the term \(\bar{y}_{ij+} -\bar{y}_{i++} -\bar{y}_{+j+} +\bar{y}_{+++}\) measures the extent to which the mean of group \(ij\) departs this null hypothesis.
In a two-way factorial design, when the data are balanced, SS[A], SS[B], and SS[AB] form a perfect decomposition of \(SS_{Groups}\). That is, \[ SS_{Groups} = SS[A] + SS[B] + SS[AB]. \]
6.2.2.5 Back to the rat data
Let’s see how this works for the rat weight-gain data. Here’s a sum-of-squares decomposition for the rat data, along with the df associated with each term in the ANOVA:
Source df SS MS
Sex 1 3781 3781
Fat 1 61204 61204
Sex*Fat 1 919 919
Error 8 11667 1458
Total 11 77570We can test for the statistical significance of the main effects of Sex and Fat, and for the interaction between Sex and Fat, by computing \(F\)-ratios. \(F\)-ratios are simply the ratio of the MS for the factor being tested divided by the MS(Error). For example, the \(F\)-ratio for the test of the interaction is \[ F = \dfrac{MS[AB]}{MSE} = \dfrac{919}{1458} = 0.63 \] We can calculate a \(p\)-value for the test of the null hypothesis that there is no interaction between the factors by comparing this statistic to an \(F\)-distribution with 1 numerator df and 8 denominator df. (The numerator and denominator df are just the number of free differences used to calculate the MS in the numerator and denominator of the \(F\) statistic, respectively.) Because larger values of the \(F\) statistic provide more evidence against the null hypothesis, \(p\)-values associated with the F-test are always one-tailed, and are the probability of observing a test statistic at least as large as the value observed. Here, the probability of observing an \(F\)-statistic with 1 ndf and 8 ddf greater than or equal to 0.63 is \(p=0.45\). The \(p\) value is large, so we have no evidence that the two factors in this experiment interact, with respect to their effect on weight gain.
We can conduct similar calculations to test for the main effects of ‘sex’ and ‘fat’, using MS[A] and MS[B], respectively. We’ll use these values to complete our ANOVA table for the rat example:
Source df SS MS F p
Sex 1 3781 3781 2.59 0.1460
Fat 1 61204 61204 42.0 0.0002
Sex*Fat 1 919 919 0.63 0.4503
Error 8 11667 1458
Total 11 77570Thus, there is no evidence of an interaction between the factors. Proceeding with an analysis of the main effects, there is no evidence that the marginal means for male vs. female rates differ (\(p=0.146\)), but there is strong evidence that the marginal means between fresh vs. rancid fat differ (\(p = 0.0002\)).
As with one-factor ANOVA, the two-factor ANOVA \(F\)-tests are usually just the beginning of our analysis. We usually want to go further and to characterize how the means differ for any signficant effect that we’ve found. In this case, because the main effect of ‘fat’ is significant, we want to go further and say more about the sign and magnitude of this effect. To do so, we’ll reformulate contrast that quantifies the main effect of fat.
\[
\theta _{fat} =\bar{\mu}_{+2} -\bar{\mu}_{+1} =\frac{\mu_{12} +\mu_{22} }{2} -\frac{\mu_{11} +\mu_{21} }{2}
\]
We’ve written this contrast as the difference between the marginal mean for rancid fat and the marginal mean for fresh fat. Thus, a positive value corresponds to rats gaining more weight when fed rancid fat, and a negative value corresponds to rats gaining more weight when fed fresh fat. Of course, we’ll usually estimate this effect and its standard error using software, but it’s worth seeing that we can do the calculation by hand if we want to be doubly sure that the software is giving the right answer. The contrast can be estimated by simply by plugging in sample means:
\[
{\hat{\theta }_{fat} =\dfrac{\bar{y}_{12+} +\bar{y}_{22+} }{2} -\dfrac{\bar{y}_{11+} +\bar{y}_{21+} }{2} } {=\dfrac{535+517}{2} -\dfrac{696+643}{2} } {=-143}
\]
Thus, we estimate that rats fed rancid fat gain 143g less weight than rats fed fresh fat. The standard error can also be computed using a modification of the formula from linear combinations for one-factor ANOVA:
\[\begin{eqnarray*}
s_{\hat{\theta}} & = & \sqrt{\left\{\frac{c_{11}^2}{n_{11}} +\frac{c_{12}^2}{n_{12}} +\frac{c_{21}^2}{n_{21}} +\frac{c_{22}^2}{n_{22}} \right\} MS_{Error} } \\
& = & \sqrt{\left\{\frac{\left(-1/2\right)^2 }{3} +\frac{\left(1/2\right)^2 }{3} +\frac{\left(-1/2\right)^2 }{3} +\frac{\left(1/2\right)^2 }{3} \right\}1458} \\
& = & 22.0
\end{eqnarray*}\]
Finally, if we wanted a 95% CI for this linear combination, we could form one by taking the appropriate critical values from a t-distribution with 8 df. (Here, 8 df because the MSE is calculated based on 8 df). Here, the appropriate critical value is 2.306, so a 95% CI for the main effect of fat is -143g \(\pm\) 2.306 \(\times\) 22.0g = (-92g, -194g).
6.2.3 Analysis using PROC GLM in SAS
We can have SAS do these calculations for us. In PROC GLM, we can obtain these calculations with the code:
proc glm data=rat;
class trt sex fat;
model food = sex fat sex*fat;
run;Edited output:
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 3 65903.58333 21967.86111 15.06 0.0012
Error 8 11666.66667 1458.33333
Corrected Total 11 77570.25000
Source DF Type III SS Mean Square F Value Pr > F
sex 1 3780.75000 3780.75000 2.59 0.1460
fat 1 61204.08333 61204.08333 41.97 0.0002
sex*fat 1 918.75000 918.75000 0.63 0.4503Let’s note the following:
- In the model statement, we can use a vertical bar as shorthand for including both main effects and interactions. The code below would produce identical output to the code above:
proc glm data=rat;
class trt sex fat;
model food = sex|fat;
run;PROC GLM provides two tables. The first is the sum-of-squares breakdown and associated ANOVA F-test if we were just treating the data as a one-factor ANOVA. That is, the \(F\)-test in the first table is a test of \(H_0\): \(\mu_{11} =\mu_{12} =\mu_{21} =...=\mu_{ab}\). (This is equivalent to a model-utility test in multiple regression.) The second table of output provides \(F\)-tests for the main and interaction effects.
PROC GLM provides two sum-of-squares decompositions, one which it calls Type I and another which it calls Type III. Type I and Type III sum-of-squares are identical for balanced factorial designs. They are not identical for unbalanced designs. We will discuss the differences for unbalanced designs later.
We can also have PROC GLM calculate linear combinations of cell means for us. To do so, though, we need to understand the effects-model coding that PROC GLM uses to represent the two-factor ANOVA model.
6.2.4 Effects notation for the two-factor ANOVA
For a two-factor ANOVA, we extend our effects-model notation in the following way: \[ \mu_{ij} =\mu +\alpha_i +\beta_j +\left(\alpha \beta \right)_{ij} \] Here, \(\mu\) is the reference level, \(\alpha_i\) is the “effect” of level \(i\) of factor A, \(\beta_j\) is the “effect” of level \(j\) of factor B, and \(\left(\alpha \beta \right)_{ij}\) is the interaction between level \(i\) of factor A and level \(j\) of factor B. In one-factor ANOVA, we saw that it was not possible to estimate all the \(\alpha_i\)’s uniquely, so we had to impose a constraint. A similar phenomenon prevails in the two-factor model. How many constraints do we need? The key equivalence is that the number of effects parameters that we can estimate is equal to the number of df for each effect in the df accounting.
Again, PROC GLM uses set-to-zero constraints. We can see the constraints by calling for SAS’s parameter estimates with the SOLUTION option to the MODEL statement in PROC GLM:
proc glm data=rat;
class trt sex fat;
model food = sex|fat / solution;
run;
The GLM Procedure
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 535.3333333 B 22.04792759 24.28 <.0001
sex female -18.0000000 B 31.18047822 -0.58 0.5796
sex male 0.0000000 B . . .
fat fresh 160.3333333 B 31.18047822 5.14 0.0009
fat rancid 0.0000000 B . . .
sex*fat female fresh -35.0000000 B 44.09585518 -0.79 0.4503
sex*fat female rancid 0.0000000 B . . .
sex*fat male fresh 0.0000000 B . . .
sex*fat male rancid 0.0000000 B . . .
NOTE: The X'X matrix has been found to be singular, and a generalized inverse was used to
solve the normal equations. Terms whose estimates are followed by the letter 'B'
are not uniquely estimable.Now, to calculate the main effect of fat using SAS, we have to recode our linear combination in terms of the parameters in the effects model. Here goes: \[\begin{eqnarray*} \theta _{fat} & = & \frac{1}{2} \left(\mu_{12} +\mu_{22} -\mu_{11} -\mu_{21} \right) \\ & = & \frac{1}{2} \left(\mu +\alpha _{1} +\beta _{2} +\left(\alpha \beta \right)_{12} +\mu +\alpha _{2} +\beta _{2} +\left(\alpha \beta \right)_{22} -\mu -\alpha _{1} -\beta _{1} -\left(\alpha \beta \right)_{11} -\mu -\alpha _{2} -\beta _{1} -\left(\alpha \beta \right)_{21} \right) \\ & = & \frac{1}{2} \left(2\beta _{2} +\left(\alpha \beta \right)_{12} +\left(\alpha \beta \right)_{22} -2\beta _{1} -\left(\alpha \beta \right)_{11} -\left(\alpha \beta \right)_{21} \right) \\ & = & -\beta _{1} +\beta _{2} -\frac{1}{2} \left(\alpha \beta \right)_{11} +\frac{1}{2} \left(\alpha \beta \right)_{12} -\frac{1}{2} \left(\alpha \beta \right)_{21} +\frac{1}{2} \left(\alpha \beta \right)_{22} \end{eqnarray*}\] Now we can read off the coefficients from the last line of the expression above and feed them into an ESTIMATE statement. Note that this combination only involves parameters for the ‘fat’ effect and the interaction:
proc glm data=rat;
class trt sex fat;
model food = sex|fat;
estimate 'Fresh v. rancid' fat -1 1 sex*fat -.5 .5 -.5 .5;
run;
Parameter Estimate Standard Error t Value Pr > |t|
Fresh v. rancid -142.833333 22.0479276 -6.48 0.0002As always, SAS provides (for free) a \(p\)-value for the test of \(H_0\): \(\theta =0\) vs. \(H_a\): \(\theta \ne 0\). For illustration’s sake, we can also write linear combinations for the main effect of sex, and for the interaction effect. One way to write these linear combinations is: \[\theta _{sex} =\frac{\mu_{21} +\mu_{22} }{2} -\frac{\mu_{11} +\mu_{12} }{2} \] and \[\theta _{int} =\left(\mu_{22} -\mu_{12} \right)-\left(\mu_{21} -\mu_{11} \right)\] Using PROC GLM, we estimate these effects as
proc glm data=rat;
class trt sex fat;
model food = trt;
estimate 'Fresh v. rancid' fat -1 1 sex*fat -.5 .5 -.5 .5;
estimate 'Male v. female' sex -1 1 sex*fat -.5 -.5 .5 .5;
estimate 'Interaction' sex*fat 1 -1 -1 1;
run;
Parameter Estimate Standard Error t Value Pr > |t|
Fresh v. rancid -142.833333 22.0479276 -6.48 0.0002
Male v. female -35.500000 22.0479276 -1.61 0.1460
Interaction 35.000000 44.0958552 0.79 0.4503Thus, to summarize our analysis of this experiment: There is no evidence of a statistically significant sex effect. There is strong evidence of an effect of fat on food consumption (\(F_{1,8} = 41.97\), \(p=0.0002\)). Rats fed rancid fat consumed on average 142.9g (s.e. 22.0g) less food than rats fed fresh fat.
Just as with one-factor ANOVA, the effects notation also gives us another way to write the null hypotheses for the main effects and interaction effects. The test of the main effects of factor A is equivalent to a test of \[ H_{0} :\alpha _{1} =\alpha _{2} =...=\alpha _{a} =0. \] The test of the main effects of factor B is equivalent to a test of \[ H_{0} :\beta _{1} =\beta _{2} =...=\beta _{b} =0. \] Finally, the test the interaction between factors A and B is equivalent to a test of \[ H_{0} :\left(\alpha \beta \right)_{11} =\left(\alpha \beta \right)_{12} =...=\left(\alpha \beta \right)_{ab} =0. \]
6.2.5 A second example when the interaction is significant
This example is taken from Steel, Torrie, and Dickey (1997). In their words,
Wilkinson (1954) reports the results of an experiment to study the influence of time of bleeding and diethylstilbestrol (an estrogenic compound) on plasma phospholipid in lambs. Five lambs were assigned at random to each of four treatment groups; treatment combinations are for morning and afternoon bleeding and with and without diethylstilbestrol treatment.
An interaction plot of the data is shown below.
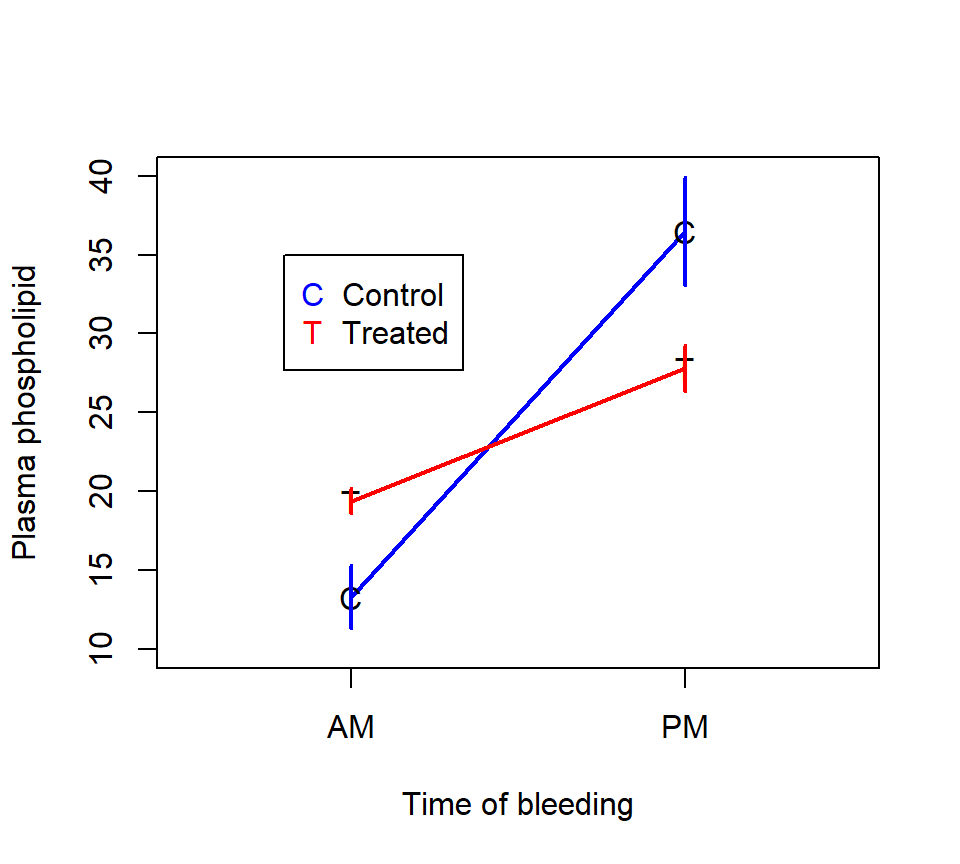
Here is the output of a two-factor ANOVA model using PROC GLM:
proc glm data=sheep;
class time drug trt;
model y = time|drug;
run;
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 3 1539.406600 513.135533 21.61 <.0001
Error 16 379.923280 23.745205
Corrected Total 19 1919.329880
Source DF Type III SS Mean Square F Value Pr > F
time 1 1256.746580 1256.746580 52.93 <.0001
drug 1 8.712000 8.712000 0.37 0.5532
time*drug 1 273.948020 273.948020 11.54 0.0037In contrast to the rat example, the interaction here is statistically significant. Because the interaction is significant, the \(F\)-tests of the main effects may no longer have a clear interpretation. Instead, we’ll analyze the simple effects of the two factors by estimating the linear combinations associated with each:
proc glm data=sheep;
class time drug trt;
model y = time|drug;
estimate 'Simple effect of time, drug=no' time 1 -1 time*drug 1 0 -1 0;
estimate 'Simple effect of time, drug=yes' time 1 -1 time*drug 0 1 0 -1;
estimate 'Simple effect of drug, time=AM' drug -1 1 time*drug -1 1 0 0;
estimate 'Simple effect of drug, time=PM' drug -1 1 time*drug 0 0 -1 1;
run;
Parameter Estimate Error t Value Pr > |t|
Simple effect of time, drug=no -23.2560000 3.08189585 -7.55 <.0001
Simple effect of time, drug=yes -8.4520000 3.08189585 -2.74 0.0145
Simple effect of drug, time=AM 6.0820000 3.08189585 1.97 0.0660
Simple effect of drug, time=PM -8.7220000 3.08189585 -2.83 0.0121Here is a partial interpretation of these contrasts. Sheep with blood drawn in the afternoon have more plasma phospholipid than sheep with blood drawn in the morning, regardless of whether the sheep were given the drug. However, the magnitude of the effect of timing is smaller on sheep given the drug (estimated effect = 8.5 units, s.e. = 3.1) than it is on sheep not given the drug (estimated effect = 23.3 units, s.e.=3.1). For sheep with blood drawn in the afternoon, the drug decreases plasma phospholipid relative to the control (estimated effect = 8.7 units less with the drug, s.e. = 3.1). For sheep with blood drawn in the morning, there is only weak evidence that the drug has an effect on plasma phospholipid (estimated effect = 6.1 units more with the drug, s.e. = 3.1, \(p=0.066\)).
6.3 \(a \times b\) factorial designs
6.3.1 Example without a significant interaction
Oehlert (problem 8.5) reports the following data. Low and Bin Mohd. Ali (1985) studied the collection of pine oleoresin by tapping the trunks of pine trees. Tapping involves cutting a hole in the tree trunk and collecting resin that seeps out. This experiment compared four shapes of holes (circle, diagonal, check, or rectangle) and the efficacy of acid (added vs. control) in collecting resin. Twenty-four pine trees were selected from a plantation and were randomly assigned to each of the 8 possible combinations of hole shape and acid. The response is total grams of resin collected from the hole. The data that we will work with are not the actual data but are instead a hypothetical data set for the same design. This is a balanced, replicated 4 \(\times\) 2 factorial experiment with treatment combinations assigned in a CRD. We’ll extend our ideas from the analysis of the 2 \(\times\) 2 factorial experiments to this 4 \(\times\) 2 factorial experiment. First, visualize the effects of the two factors with an interaction plot: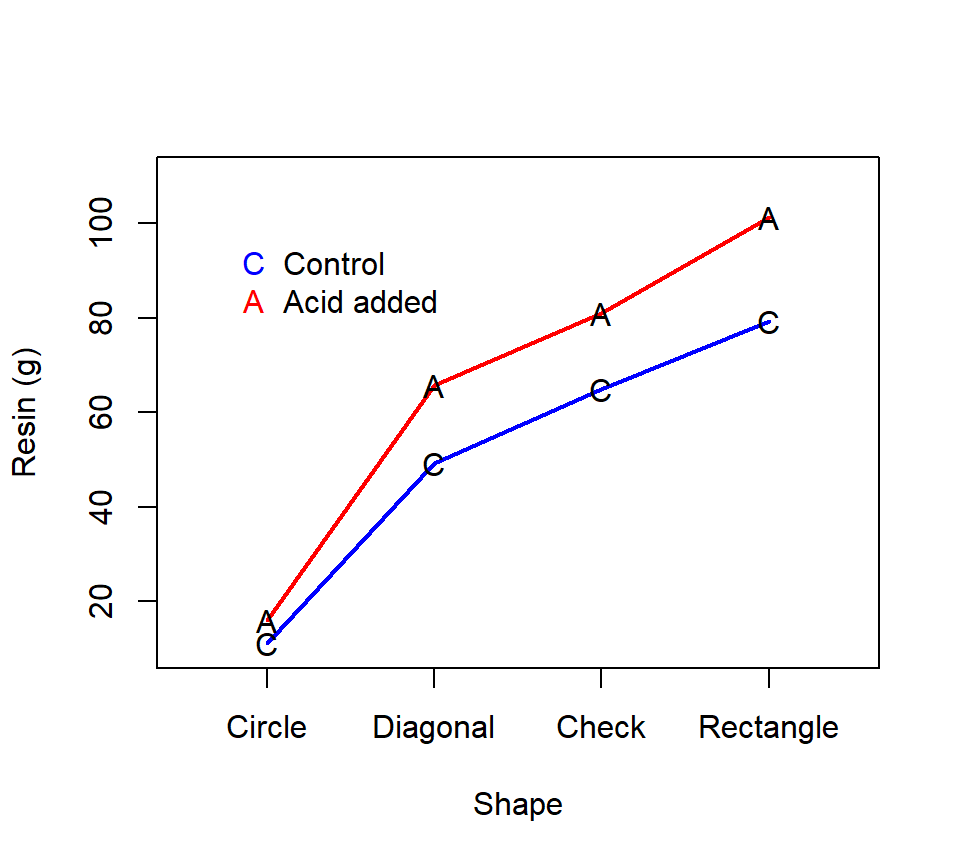
Our notation here will be similar to the 2 \(\times\) 2 factorial design, except that now we’ll allow an arbitrary number of levels for the two crossed experimental factors. Our strategy for analyzing data from a \(a \times b\) factorial design will still be to use a sum-of-squares decomposition to test for interaction effects and/or main effects of the two factors. As with a 2 \(\times\) 2 design, when the data are balanced, the sum-of-squares for the groups can be exactly partitioned into the three components using the formulas that we introduced before:
\[
SS_{Groups} = SS[A] + SS[B] + SS[AB]
\]
For the oleoresin data, this decomposition is
| source | df | SS |
|---|---|---|
| Shape | 3 | 19407 |
| Acid | 1 | 1305 |
| Shape*Acid | 3 | 237 |
| Error | 16 | 721 |
| Total | 23 | 21672 |
| source | df | SS | MS | \(F\) | \(p\) |
|---|---|---|---|---|---|
| Shape | 3 | 19407 | 6469 | 143.5 | <0.0001 |
| Acid | 1 | 1305 | 1305 | 29 | <0.0001 |
| Shape*Acid | 3 | 237 | 79.2 | 1.76 | 0.1961 |
| Error | 16 | 721 | 45.1 | ||
| Total | 23 | 21672 |
Thus, this two-factor ANOVA shows that there is no statistical evidence of an interaction (\(F_{3, 16} = 1.76\), \(p = 0.20\)). Because the interaction is not significant, it makes sense to analyze main effects. There is very strong evidence of a main effect of shape (\(F_{3, 16} = 143.5\), \(p < 0.0001\)) and a main effect of the acid treatment (\(F_{1, 16}\) = 29.0, \(p < 0.0001\)). Because the main effects are significant (and the interaction is not significant), then we can use linear contrasts and multiple comparisons procedures to analyze the marginal means of both factors just as we would in a one-factor layout. For example, we could use a MEANS statement to compare treatment means using multiple comparisons. Here is code for a Tukey’s HSD comparison of the marginal means for the hole shapes:
proc glm data=resin;
class shape acid;
model resin = shape acid shape*acid;
means shape / tukey;
run;
Tukey's Studentized Range (HSD) Test for resin
Means with the same letter are not significantly different.
Tukey
Grouping Mean N shape
A 90.333 6 rectangl
B 73.000 6 check
C 57.500 6 diagonal
D 13.667 6 circularThus, all of the shapes are significantly different from one another.
6.3.2 Example with a significant interaction
Here’s a second example of a \(a \times b\) factorial design where the interaction is significant (based off of exercise 15.24 in Ott and Longnecker (2015)): An experiment was performed to compare the effect of soil pH and calcium additives on trunk diameters of orange trees. 36 trees were selected at random from an orange grove. Experimental treatments were arranged in a factorial design, with 4 levels of soil pH and 3 levels of calcium supplement. Treatment combinations were assigned to trees at random in a balanced CRD, with three trees per treatment combination.
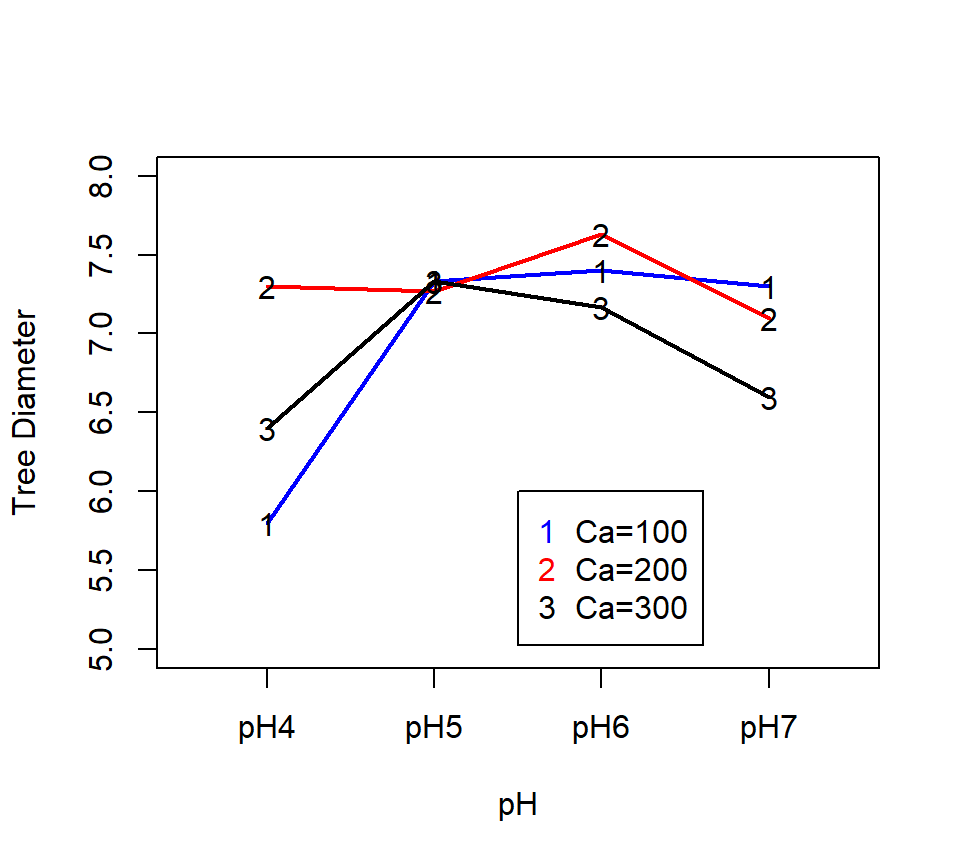Here is a two-factor ANOVA analysis in SAS:
proc glm data=orange;
class pH calcium;
model diameter = pH calcium pH*calcium;
run;
The GLM Procedure
Dependent Variable: diameter
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 11 9.18305556 0.83482323 12.32 <.0001
Error 24 1.62666667 0.06777778
Corrected Total 35 10.80972222
Source DF Type III SS Mean Square F Value Pr > F
pH 3 4.46083333 1.48694444 21.94 <.0001
calcium 2 1.46722222 0.73361111 10.82 0.0004
pH*calcium 6 3.25500000 0.54250000 8.00 <.0001There is strong evidence of an interaction. Because of the significant interaction, we analyze simple effects. There are multiple ways to analyze simple effects. With more than two levels of each factor, we might consider \(F\)-tests of the cell means associated with each level of one of the two factors. For example, we could ask whether the responses differ among the pH levels when calcium = 100. That is, we could test \[ H_0: \ \ \mu_{11} =\mu_{21} =\ldots =\mu_{41}. \] More generally, we can test for equality across the levels of factor A for each level of factor B: \[ H_0: \ \ \mu_{1j} =\mu_{2j} = \ldots =\mu_{aj}. \] We can also test for equality across the levels of factor B for each level of factor A: \[ H_0: \ \ \mu_{i1} =\mu_{i2} =...=\mu_{ib}. \] These tests are implemented in SAS using the SLICE option of the LSMEANS statement. (Note: LSMEANS calculates the Least Squares Means of each treatment level. LSMEANS and MEANS coincide for balanced data, but only LSMEANS has the SLICE option implemented.)
proc glm data=orange;
class pH calcium;
model diameter = pH calcium pH*calcium;
lsmeans pH*calcium / slice=pH slice=calcium;
run;
pH*calcium Effect Sliced by pH for diameter
Sum of
pH DF Squares Mean Square F Value Pr > F
4 2 3.606667 1.803333 26.61 <.0001
5 2 0.008889 0.004444 0.07 0.9367
6 2 0.326667 0.163333 2.41 0.1112
7 2 0.780000 0.390000 5.75 0.0091
Sum of
calcium DF Squares Mean Square F Value Pr > F
100 3 5.382500 1.794167 26.47 <.0001
200 3 0.446667 0.148889 2.20 0.1146
300 3 1.886667 0.628889 9.28 0.0003The first table above tests for differences among the calcium levels within each of the 4 pH levels. This table shows that there are significant differences between calcium levels for pH=4 and pH=7, but not for pH=5 or pH=6. The second table shows tests for differences between the pH levels within each of the three calcium levels. This table shows that there are significant differences between the pH levels when calcium=100 and when calcium=300, but not when calcium=200.
We could then explore each of the significant differences above in more depth by using linear contrast or multiple comparisons. For example, suppose we wanted to compare calcium=200 vs. calcium=100 when pH=4. We define a suitable linear contrast as \[ \theta =\mu_{11} -\mu_{12} \] and estimate it in SAS by figuring out the appropriate effects parameters: \[\begin{eqnarray*} \theta & = & \mu_{11} -\mu_{12} \\ & = & \left( \mu + \alpha_1 + \beta_1 + (\alpha \beta)_{11} \right) - \left( \mu + \alpha_1 + \beta_2 + (\alpha \beta)_{12} \right) \\ & = & \beta_1 - \beta_2 + (\alpha \beta)_{11} - (\alpha \beta)_{12} \end{eqnarray*}\]
proc glm data=orange;
class pH calcium;
model diameter = pH calcium pH*calcium;
estimate 'Ca100 vs Ca200 when pH=4' calcium 1 -1 pH*calcium 1 -1;
run;
Standard
Parameter Estimate Error t Value Pr > |t|
Ca100 vs Ca200 when pH=4 -1.53333333 0.21256807 -7.21 <.00016.4 Unreplicated factorial designs
Consider an experiment with 5 levels of factor A, 3 levels of factor B, and a single observation for each treatment combination. This is called an unreplicated design because there is only a single replicate for each treatment combination. Let’s try a df accounting for a model that includes main effects of both factors and an interaction:| source | df |
|---|---|
| Factor A | 4 |
| Factor B | 2 |
| A*B interaction | 8 |
| Error | 0 |
| Total | 14 |
This model has no df remaining to estimate the experimental error. Consequently, we cannot estimate \(MS_{Error}\) and hence we cannot conduct \(F\)-tests of the treatment effects.
One option with unreplicated designs is to assume that there is no interaction between the two experimental factors. A model without an interaction is called an additive model. In effects notation, the model is: \[ y_{ijk} =\mu +\alpha_i +\beta_j +\varepsilon _{ijk} \] With an additive model, we use the df that had been allocated to the interaction to estimate the experimental error instead:| source | df |
|---|---|
| Factor A | 4 |
| Factor B | 2 |
| Error | 8 |
| Total | 14 |
The additive model can be used to test for effects of factors A and B. Obviously, these tests are only trustworthy if the assumption of no interactions is appropriate. In biology, it is usually risky to assume that there are no interactions between experimental factors. Additive models for unreplicated designs are more common in industrial statistics.
John Tukey developed a test for additivity with unreplicated factorial designs, sometimes called Tukey’s single degree-of-freedom test. We will not cover Tukey’s test in ST512, although you may want to read about it on your own if you need to analyze an unreplicated factorial design in your own research.
6.5 Missing cells
An extreme case of unbalanced data occurs when there are no observations for one or more treatment combinations. For example, consider the sheep data used to illustrate an interaction in a 2 \(\times\) 2 factorial design, but suppose that there were no data for control sheep whose blood was drawn in the morning. We say that the ``cell’’ representing the treatment combination of control x morning bleeding is missing.
There are three options for missing cells designs:
Remove one of the levels of one experimental factor to eliminate the missing cell. In the example above, we could eliminate the data from the drugged sheep whose blood was drawn in the morning, and just compare the sheep with blood drawn in the afternoon to look for a simple effect of drug vs. control. Or, we could eliminate the data from the control sheep with blood drawn in the afternoon, and just look for a simple effect of morning vs. afternoon bleeding for sheep given the drug.
Treat the design as a one-factor layout, where each treatment combination is a separate level of the single experimental factor.
Use an additive model.
6.6 More than two factors
All of these ideas can be extended to factorial experiments with more than two factors.
Example (based off of an example in Rao (1998)): An investigator is interested in understanding the effects of water temperature (cold vs. lukewarm vs. warm), light (low vs. high), and water movement (still vs. flowing) on weight gain in fish. She has 24 aquaria to serve as experimental units. Each of the 3 x 2 x 2 = 12 treatment combinations are randomly assigned to 2 of the 24 aqauria, and the average weight gain of the fish in each aquaria is measured. This is a balanced three-way factorial design with a CRD randomization structure.
As a first attempt to get a handle on these data, let’s make three different interaction plots, one for each water temperature:
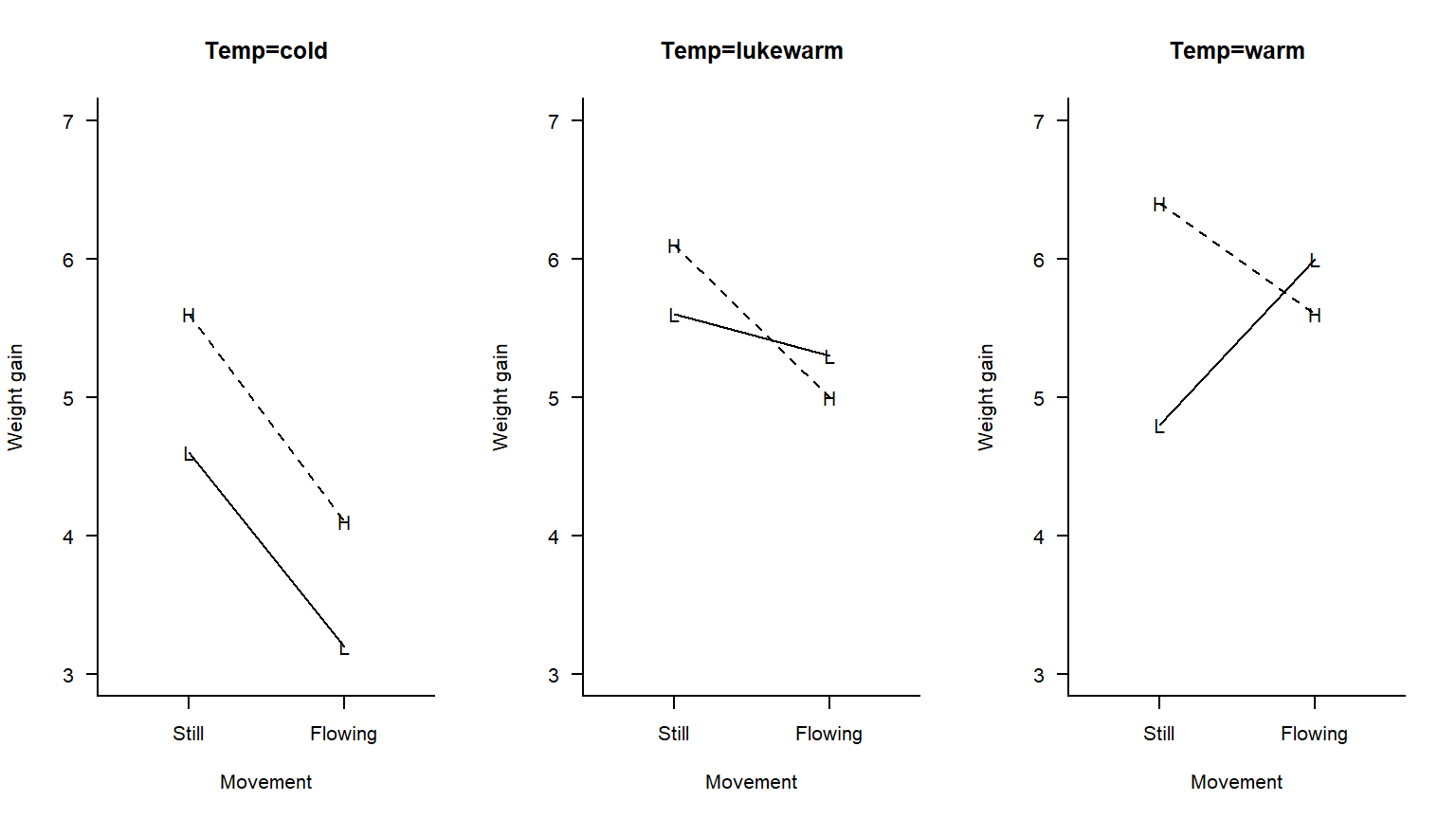The interaction plot suggests that for some water temperatures, there is an interaction between light levels and water movement. Thus, the way in which the effect of light depends on water movement depends in turn on temperature. Yikes! This is a three-factor interaction. We need a test to see if this interaction is statistically significant, or if it can be attributed to experimental error.
To develop notation for the three-factor model, we’ll extend our ideas from two factor models. For example, \(\mu_{ijk}\) will denote the unknown population mean for the combination of level \(i\) of factor A, level \(j\) of factor B, and level \(k\) of factor C.
With three factors, there are two possible types of interactions:
First-order interactions}: Interactions between two factors
Second-order interactions}: Interactions between first-order interactions
For example, in this experiment the first-order interaction between light level and water movement might describes how the effect of light depends on water movement and vice versa. The second-order interaction describes how this first order interaction may in turn depend on water temperature.
Note that the rules for determining the df associated with higher-order interactions are the same as for first-order interactions: the df are always equal to the product of the df associated with each constituent factor. (Think of this in terms of regression with indicator variables again.)
In effects notation, we can write the cell means as \[ \mu_{ijkl} =\mu +\alpha_i +\beta_j +\gamma _{k} +\left(\alpha \beta \right)_{ij} +\left(\alpha \gamma \right)_{ik} +\left(\beta \gamma \right)_{jk} +\left(\alpha \beta \gamma \right)_{ijk} \] Here, the parameters denoted by \(\left(\alpha \beta \gamma \right)_{ijk}\) capture the second-order interaction among the three factors.
proc glm data=fishgrowth;
class light temp movement;
model gain = light|temp|movement;
run;
Example of 3x2x2 factorial from Rao 2
Dependent Variable: gain
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 11 17.94458333 1.63132576 5.60 0.0030
Error 12 3.49500000 0.29125000
Corrected Total 23 21.43958333
Source DF Type III SS Mean Square F Value Pr > F
light 1 2.10041667 2.10041667 7.21 0.0198
temp 2 7.64333333 3.82166667 13.12 0.0010
light*temp 2 0.64333333 0.32166667 1.10 0.3629
movement 1 2.47041667 2.47041667 8.48 0.0130
light*movement 1 1.35375000 1.35375000 4.65 0.0521
temp*movement 2 2.89333333 1.44666667 4.97 0.0268
light*temp*movement 2 0.84000000 0.42000000 1.44 0.2746The analysis strategy with a three-way factorial design is similar to the analysis strategy with a two-way factorial design:
Test for the significance of the second-order interaction.
If the second-order interaction is significant, either unpack the factorial treatment structure and treat the design a one-factor ANOVA, or ``divide and conquer’’ by analyzing the effects of two factors at each level of the third factor.
If the second-order interaction is not significant, you may remove the second-order interaction and re-fit the model, although this is not necessary. Test for the significance of the first-order interactions. If any of the first-order interactions are significant, analyze simple effects. If none of the first-order interactions are significant, analyze main effects.
In the example above, the second-order interaction is not statistically significant (\(F_{2, 12} = 1.44\), \(p = 0.27\)). The only statistically significant first-order interaction is the interaction between water temperature and movement (\(F_{2,12} = 4.97\), \(p = 0.027\)). Neither of the first-order interactions involving light are statistically significant (although the light-by-movement interaction is on the border of statistical significance, \(F_{1,12} = 4.65\), \(p = 0.052\)). The main effect of light is statistically significant (\(F_{1,12} = 7.21\), \(p = 0.020\)). We could then proceed by quantifying the main effect of light with a linear combination, and quantifying the simple effects of movement at different water temperatures.
Main effect of light: \[\theta _{light} =\bar{\mu}_{1++} -\bar{\mu}_{2++} \] Simple effect of movement when temperature = cold: \[\theta _{m/C} =\bar{\mu}_{+11} -\bar{\mu}_{+12} \] Simple effect of movement when temperature = lukewarm: \[\theta _{m/L} =\bar{\mu}_{+21} -\bar{\mu}_{+22} \] Simple effect of movement when temperature = warm: \[\theta _{m/W} =\bar{\mu}_{+31} -\bar{\mu}_{+32} \]
A final note: unreplicated three-way factorial designs are not uncommon in the life sciences. To analyze these designs, one typically assumes that there is no second-order interaction, and uses the df that would have been absorbed by the second-order interaction as the df for error. Some will argue that higher-order interactions are rare in nature, and thus assuming that they do not occur is justified. Whether you agree with this or view it as a just-so rationalization is up to you.